Functional JavaScript Part 1: Lists

Functional programming may seem like a buzzword or fad, but there are good reasons why so many companies and frameworks are hopping on board these days, *cough* Facebook *cough*. Functional programming has been around for a long time now actually and shows no signs of stopping. It is simply elegant at times, naturally expressing problems and their solutions in terms of what instead of how.

Thankfully, JavaScript is already capable of equipping programmers with powerful functional programming constructs. So, I would like to take some time to go through a short post series on functional programming (FP). In this first post, I will go over the classic case study of the power of FP, the list. We will discover the beauty of building and iterating lists through two keystone FP concepts, recursion and immutability.

Recursion and Immutability

In case you are unfamiliar with recursion and immutability, we will expound upon them for a minute.

According to Wikipedia: “Recursion is the process of repeating items in a self-similar way.”

In terms of FP, this is the action of a function calling itself a number of times. OK… but what does that accomplish? Well, one classic example is implementing a function to calculate the value of the Fibonacci sequence at a given number n:

function fib(n) {
  if (n < 2) {
    return n;
  }
 
  return fib(n - 1) + fib(n - 2);
}

Notice that we call our fib function inside itself for inputs n > 1. We return the result of fib(n - 1) + fib(n - 2) to get the final answer. If we were to trace calls to fib for n = 4, we would see something like this:

fib(4)
fib(3) + fib(2)
fib(2) + fib(1) + fib(1) + fib(0)
fib(1) + fib(0) + 1 + 1 + 0
1 + 0 + 1 + 1 + 0
3

Notice something interesting? At the next to last line, all that is left is addition with 1's and 0's to yield 3. This is the power of recursion, the base case.

Think of recursion in terms of a tree. At the root of our tree is the base case(s). For fib, our base cases are 1 and 0, so they comprise the root of the tree. From the root, the tree grows out into branches and leaves. Those leaves are our values for n > 1. We cannot have the leaves without the root, so we cannot have these answers without our base cases.

Imagine if we wanted to traverse the life source of that leaf. We would start at the leaf, working our way down the branches and trunk step-by-step to finally arrive at the root. That is like our growing call stack with recursive calls to finally get to something that returns an actual value, 1 or 0. Then, everything cascades back up to give us our final value, which is 3 in the case of n = 4.

Now compare this to an imperative approach with dynamic programming:

function fib(n) {
  if (n < 2) {
    return n;
  }
 
  var n0 = 0;
  var n1 = 1;
  var ans = 0;
 
  for (var i = 2; i <= n; i++) {
    ans = n0 + n1;
    n0 = n1;
    n1 = ans;
  }
 
  return ans;
}

That is a little less understandable, albeit FAAAARRR more performant. If we compare the imperative approach with the functional approach, we find that the functional approach more naturally expresses the recurrence relation of the Fibonacci sequence, $F_n = F_{n - 1} + F_{n - 2}$, where $F_0 = 0$ and $F_1 = 1$. The recurrence relation is in the imperative approach too, but we have to look a little harder.

That briefly covers recursion, but what about immutability? Let us compare the two implementations of our fib function again. You will notice that our imperative approach modifies the value of several variables multiple times. We increment i and reassign values to ans, n0, and n1. Our functional approach never reassigns values to anything. In fact, the only variable in our functional implementation is our one n parameter, and we never change it.

When we do not change the values of our state (i.e. our variables), we are enforcing immutability. The converse, mutability, is when we mutate state (i.e. change the value of variables). Immutability is a key tenet of FP. It allows us to think of our functions in simpler terms: single input, single output, no side effects. This can help us produce fewer bugs (take that with a grain of salt) and make testing easier.

The List

With that introduction to recursion and immutability behind us, we can now focus on our task of building the functional list.

So, what is a list? I am sure most of you are already familiar with the concept of linked lists, and this is not very different. We will have a head, the first item in a list, and a tail, the remaining items in the list. Typically, we use some data structure that wraps the actual value and has a pointer or reference to the next item in the list. We know we are at the end of the list when the last item points to some null reference.

Imagine we have a linked list of integers. We would typically view it like so:

Functional lists are pretty much the same thing, but we adopt some different conventions when referring to them. Typically, we refer to our wrapping data structure as a “cons cell”. There are built-in operators and functions in functional languages to build a cons cell. The cons operation takes two arguments, a head and a tail. The head is the actual underlying value and the tail is the reference to the next cons cell.

The final item in the list will have a tail that points to nil, or the empty list. This is the null value at the end of the linked list. It is that final nil reference that really makes the top level cons cell a “list.”

Now, when it comes to functional lists, I like to picture them differently. I like to view each item’s tail as a literal tail of the remaining items instead of just a reference to the next item. I like to imagine a recursive (there is that word again) data structure of cons cells wrapping other cons cells until we get to the final empty list. Treating this as a recursive data structure is hugely powerful! Just look below; you may even see why that tree analogy is so important.

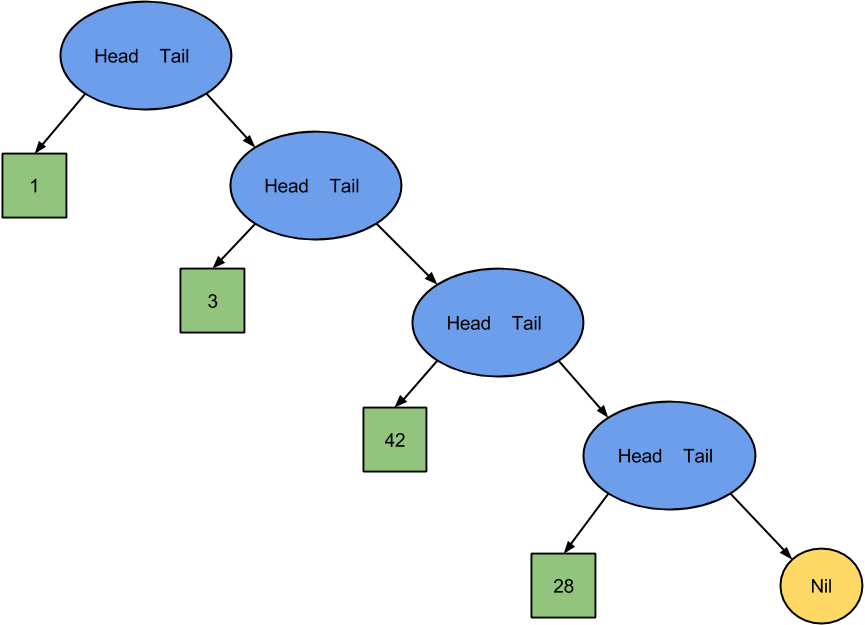
When we think back to our tree analogy, this illustration suggests something powerful about lists as recursive data structures. Notice the similarities with our Fibonacci function call stack. We now think of our list in terms of what it is built up from: the empty list.

With this revelation, we can begin to implement functions to operate on our list. We will look at two classic functions, map and reduce, and create our own recursive implementations of them for our list.

Implementing the List

First, we need to create our list data structure. To accomplish this, we actually need to implement the cons cell and nil, the empty list.

var Cons = function(head, tail) {
  this.head = head;
  this.tail = tail;
};
 
Cons.prototype.isEmpty = false;

var Nil = {
  isEmpty: true,
 
  get head() {
    throw new Error('Accessing head on empty list.');
  },
 
  get tail() {
    throw new Error('Accessing tail on empty list.');
  }
};

So, Cons has a head property, a tail property, and isEmpty = false. Notice that Nil is an object literal instead of a constructor function. It does not make sense to make multiple instances of Nil when it always represents the empty list. This is no different than the null value in programming languages. Also notice that since Nil is the empty list, isEmpty = true, and we throw errors if you try to access head or tail on it.

So, if we wanted to build a list, we could do this then:

var list = new Cons(1, new Cons(3, new Cons(42, new Cons(28, Nil))));

That is unsightly, though. We should at least introduce a helper function to clean it up a little:

var cons = function(head, tail) {
  return new Cons(head, tail);
};
 
var list = cons(1, cons(3, cons(42, cons(28, Nil))));

That is better; we will create an even nicer-looking function later on, but we will use this for now.

Implementing Map and Reduce

Now we are ready to create our own implementations of map and reduce. If you are unfamiliar with these functions, I encourage you to check out the examples at the Mozilla developer website for JavaScript arrays: map and reduce.

Briefly, map takes a list, applies some transformation function to each item, and returns a new list of those transformed items. reduce takes a list and transforms the list (reduces the list) to some other value by applying the transformation function to each item in the list.

We will implement these functions in two manners, first as regular functions and then as methods of our Cons and Nil objects. First, let us look at map.

Map

var map = function(list, fn) {
  if (list.isEmpty) {
    return list;
  }
 
  return cons(fn(list.head), map(list.tail, fn));
};

So what is going on here? Just like our functional fib implementation and with almost any FP function, we need a base case. Remember that this is the root from which we build our result. In this instance, our base case is Nil. We check that via the isEmpty property. If it is true, then we just return list (we could return Nil here too since they are the same object).

Now let us dissect the meat of this function at line 6. This is a map function, so we have to apply the supplied function argument fn to each value. We do that by calling fn(list.head). Because we need to apply the function to every item, we then recursively call map with the remaining items, which are referenced by list.tail. Therefore, we call map(list.tail, fn). Finally, we wrap those two calls in cons, returning cons(fn(list.head), map(list.tail, fn)). Notice anything else? We are returning a new cons cell. We never modified our original list, so we are upholding immutability too.

If we follow the recursive calls, we will see our call stack keep growing until we finally get to Nil. Once we return it, we can begin to return the result for each remaining frame in the stack until the first call returns the new list. Here is how the list will get built with each call below:

var list = cons(1, cons(2, cons(3, Nil)));
var double = (n) => n * 2;
 
map(list, double); // yields:
 
cons(2, map(cons(2, cons(3, Nil)), double));
cons(2, cons(4, map(cons(3, Nil), double)));
cons(2, cons(4, cons(6, map(Nil, double))));
cons(2, cons(4, cons(6, Nil)));

There is our first implementation of map. But what if we wanted to utilize JavaScript’s object-oriented capabilities and eliminate that isEmpty conditional check? In this case we need to add map as a method to the Cons prototype and to the Nil object.

Cons.prototype.map = function(fn) {
  return cons(fn(this.head), this.tail.map(fn));
};
 
Nil.map = function() {
  return this;
};

Basically what we have done is separate out the branches of computation in map to the objects with which they are concerned. Cons#map builds up the new cons cells and Nil just returns itself. Notice we also changed map(this.tail, fn) to this.tail.map(fn). I think this looks a little nicer than the strict function implementation. In most functional programming languages, we do not have this affordance, so they utilize some rather elegant pattern matching control structures that are similar to switch statements but vastly more powerful.

Our usage would only change in how we initially call map:

var list = cons(1, cons(2, cons(3, Nil)));
var double = (n) => n * 2;
 
list.map(double); // cons(2, cons(4, cons(6, Nil)))

So that is map. See how elegantly and simply we were able to implement it in just a couple lines. An imperative approach would require some looping construct and constantly reassigning values to create a new list, which means more code that may be harder to reason about (some people may find looping more intuitive, so I do not want to discredit them).

Reduce

Next up is reduce. Recall that with reduce we want to transform our list into some other value and that may not be another list. Here is the function implementation:

var reduce = function(list, fn, memo) {
  if (list.isEmpty) {
    return memo;
  }
 
  return reduce(list.tail, fn, fn(memo, list.head));
};

This is very similar to our map implementation. Notice that we have one more input this time, memo. Think of this as an accumulator, so we can keep track of the value that we are building from our list. Also notice that memo will serve as the value for our base case, the empty list. This is where we check isEmpty again.

If our list is not empty, then we of course make a recursive call to reduce, passing in the tail, the same transformation function fn, and the recalculated memo value fn(memo, list.head). The combination of recursive calls and calculating new memo values is what allows us to transform the entire list into something else.

Here is a great example where we can calculate the sum of a list of numbers:

var list = cons(1, cons(2, cons(3, Nil)));
var add = (x, y) => x + y;
 
reduce(list, add, 0); //=> 6

And of course, let us simplify our implementation with the object-oriented approach:

Cons.prototype.reduce = function(fn, memo) {
  return this.tail.reduce(fn, fn(memo, this.head));
};
 
Nil.reduce = function(fn, memo) {
  return memo;
};

If you are familiar with reduce, then you also know we could alter our implementation to not require the initial memo argument. Instead we could make it optional, and use the first head as the initial memo if none is supplied.

Now you might notice something. Is not map just a special case of reduce? Yes! In fact we can implement map in terms of reduce's cousin reduceRight. reduceRight is just like reduce except it reduces the list items in the reverse direction. So, it would first encounter Nil, then the next-to-last item, and keep going until it reaches the first item in the list. reduceRight can be implemented as follows:

Cons.prototype.reduceRight = function(fn, memo) {
  return fn(this.tail.reduceRight(fn, memo), this.head);
};
 
Nil.reduceRight = Nil.reduce;

This is very close to the implementation of reduce except we flip the order in which we call our transformation function and when we make our recursive calls. This ensures that the transformation function first gets called with Nil. This is crucial if we want to implement map in terms of reduceRight. If we used reduce instead, we would indeed map over our values, but build our new list in the reverse direction.

Our new map implementation can be seen below:

Cons.prototype.map = function (fn) {
  var consBuilder = function(memo, value) {
    return cons(fn(value), memo);
  };
 
  return this.reduceRight(consBuilder, Nil);
};

Since we are reducing from the right, we will start from Nil and build cons cells up from that. Think back to our list picture where we stacked the cons cells like a tree. Picture reduceRight and our new map implementation as stacking those cons cells from the bottom up.

Wrapping It Up

I hope this gives you an idea of the power of expressiveness inherent in functional programming. With very little code, we built an iterable list and two famous functions to operate on that list.

However, please keep in mind that these are very basic implementations and are not optimized for performance. You will also run into issues if you try to iterate over very large lists. Because we depend on recursion, our call stack could grow very large and lead to the infamous stack overflow. One way around this is to utilize tail call optimization, a feature which is slated for ES6. (Essentially, if you tailor the last statement in your function correctly, you can ensure that recursive calls do not add to the call stack but instead just replace the current stack frame with a new one.)

One more thing. I mentioned there was a way we could simplify list construction to avoid several cons calls. We can implement a list function that takes a variable number of arguments and produces a list. Since we are talking about FP, let us implement that function in a functional manner too.

var list = function () {
  if (arguments.length === 0) {
    return Nil;
  }
 
  var head = arguments[0];
  var tail = [].slice.call(arguments, 1);
 
  return cons(head, list.apply(null, tail));
};

So notice here we are mirroring the concepts we used in our list functions. We are returning Nil if arguments are empty, so this is our base case. We then get the head and tail from arguments and pass them along to a cons call. Inside that cons call we recursively apply the list function to the tail via list.apply(null, tail).

Then, we can use our list function for easier list construction:

var myList = list(1, 3, 5);
//=> cons(1, cons(3, cons(5, Nil)));
 
var myOtherList = myList.map(n => n * 3);
//=> cons(3, cons(9, cons(15, Nil)));
 
var nine = myList.reduce((x, y) => x + y);
//=> 9
 
var listOfLists = list(list(1), list(2), list(3));
//=> cons(cons(1, Nil), cons(cons(2, Nil), cons(cons(3, Nil), Nil)));
 
var flattened = listOfLists.map(innerList => innerList.head);
//=> cons(1, cons(2, cons(3, Nil)));

Thanks for reading and please leave any feedback or questions you may have on FP and lists. If you feel there are any holes in this explanation, please let me know. I hope you now have a better understanding and appreciation for what is possible with functional programming. We will continue to investigate the concepts of functional programming in future posts.